DCPY.BIRCHCLUST(n_clusters, threshold, branching_factor, columns)

Parameters

• n_clusters – Number of clusters after the final clustering step performing Agglomerative clustering, which treats the subclusters from the leaves as new samples. When None, the algorithm finds optimum number of clusters, integer (default 3).

• threshold – The radius of the subcluster obtained by merging a new sample and the closest subcluster should be lesser than this thresholds. Lower value promotes splitting and generates more subclusters. Tune it to find optimum number of clusters, float (default 0.5).

• branching factor – Maximum number of CF subclusters in each node. If a new sample enters such that the number of subclusters exceed the branching_factor, then that node is split into two nodes with the subclusters redistributed in each, integer (default 50).

• columns – Dataset columns or custom calculations.

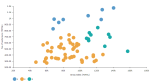
Example: DCPY.BIRCHCLUST(3, 0.5, 50, sum([Gross Sales]), sum([No of customers])) used as a calculation for the Color field of the Scatterplot visualization.

Input data

• Numeric variables are automatically scaled to zero mean and unit variance.
• Character variables are transformed to numeric values using one-hot encoding.
• Dates are treated as character variables, so they are also one-hot encoded.
• Size of input data is not limited, but many categories in character or date variables increase rapidly the dimensionality.
• Rows that contain missing values in any of their columns are dropped.

Result

• Column of integer values starting with 0, where each number corresponds to a cluster assigned to each record (row) by the algorithm.
• Rows that were dropped from input data due to containing missing values have missing value instead of assigned cluster.

Key usage points

• Use it when the number of data points is very large. When the number of variables is larger, MiniBatch K-means might be a better solution.

• It is the best available method for clustering very large data sets when considering time complexity, memory consumption, and clustering quality.

• Can both find optimum number of clusters and find specified number of clusters.

• Sensitive to highly correlated inputs
• Sensitive to data order
• Inability to deal with non-spherical clusters of varying sizes

For the whole list of algorithms, see Data science built-in algorithms.