Chord diagram

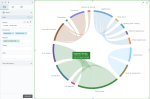
A chord diagram shows connections or flows between several dimensions. Each dimension is represented by a colored fragment on the outer part of the circular layout. The arcs between each dimension are drawn to show the connection. The size of the arc is proportional to the magnitude of the flow (based on the selected measure).

When to use

Use a chord diagram to show one-level quantitative relationships between categories and their relative magnitudes. The typical use cases are migration analysis, economic flows, and traffic flows.

Chord diagrams are visually appealing and popular but can become unreadable if you have too many dimensions and connections. Avoid over-cluttering and provide explanations where needed.

Data requirements

To build this chart, define the required and optional data fields as follows:

• Dimensions – Two dimensions (the order of dimensions matters: the first dimension is a source node and the second one is a destination node)
• Measure – One measure (to represent the size of the arc connecting dimensions)
• Tooltip – (Optional) One or more measures

Use case

The following chart shows the cost of sales for each department and how it is distributed among product lines. When pointing to the arc, you can see the tooltip showing the selected dimensions, and the measure of the flow (sales cost). When pointing to a node (the outer part of the circle), you can see the total sales cost for the respective dimension (department or product line).

References

For details on how to customize your visualization, see Visualization settings.

For a whole list of visualizations, see the following topics:

• Visualizations by function (find a visualization to suit your business case)
• Visualizations by type (find a visualization based on how it is organized on the interface)